書評『統計のための行列代数』

July 19, 2020 | 21 min read | 3,608 views

はじめに

『統計のための行列代数』（D. A. Harville 著，伊理正夫監訳，丸善出版，2012年）を読んだので，まとめと感想を書きます．

（そこまでの精読はできていませんが，それでも誤植と思われる箇所が散見されたので，気づいた範囲ですが末尾にまとめておきました．）

まとめ+α

原題は『Matrix Algebra from a Statistician’s Perspective』で，統計学者が身につけるべき線形代数の知識や考え方を全2巻でまとめた著名な教科書です．線形代数は重要かつ範囲がとても広く，抑えるべきポイントがわかりづらいと大学時代から感じていたので，こういう応用を見据えた教科書はありがたいです．
一般的な線形代数の教科書ではあまり取り上げられない射影や行列の微分，対称行列や正定値行列の諸公式などに詳しいのが特徴的だと感じました．また，すべての定理に丁寧な証明がついている（読者の演習にしたりしない）のもありがたいです．
一方で，大学1年の数学で必ずと言っていいほど登場するJordan標準形は索引に名前すらないなど，大胆に削ぎ落とされている内容もあります（確かに，Jordan標準形は大学1年生以来まだ使ったことがありません…）．固有値が導入されるのがかなり終盤だったりと，進め方の意図がわからない部分もありました．
このような理由から，線形代数の1冊目として選ぶには偏りすぎですが，統計という応用先を見据えた上での再学習には良さそうな教科書だと感じました．

以下では，他書からの補足や応用上の話も交えつつ各章の内容を簡単にまとめます．自分が後で復習するときに役立つように，という基準で内容を取捨選択しています．間違いなどありましたらコメントいただければ幸いです．

第1章行列

行列のスカラー倍や行列どうしの加減乗除といった基本的演算，および対称行列や三角行列といった用語を定義します．

第2章部分行列と分割行列

ブロック対角行列などを定義するのに必要になる部分行列と分割行列を準備します．主部分行列 (principal submatrix) とその部分集合である首座部分行列 (leading principal submatrix) は忘れがちなので掲げておきます．

主部分行列: $n \times n$ 行列から第 $i_1, \ldots, i_r$ 行と第 $i_1, \ldots, i_r$ 列を削除することで得られる $(n-r) \times (n-r)$ 部分行列
首座部分行列: 主部分行列のうち， $\{ i_k ~|~ k=1,\ldots, r\} = \{ i ~|~ i=n-r+1,\ldots,n\}$ であるもの．すなわち， $n \times n$ 行列から最後の $r$ 行と $r$ 列を削除することで得られる $(n-r) \times (n-r)$ 部分行列

対称行列の主部分行列もまた対称行列であり，三角行列の主部分行列も三角行列です．

第3章線形従属と線形独立

タイトルどおりの内容が4ページで書かれているだけです．

第4章線形空間 ―― 行空間と列空間

行（列）空間，基底，次元 (dimension)，階数 (rank)，非特異 (non-singular) といった極めて重要な概念を導入します．
ところで，行列がフルランクであることは「正則 (regular)」と呼ぶのが一般的だと思いますが，この本では「非特異 (non-singular)」という言葉を使います．否定形でわかりにくいところがありますが，統計学で使う「正則化 (regularization)」と区別するためでしょうか．

第5章（正方）行列のトレース

正方行列に対して定義されるトレースを導入します．行列 $\textbf{A}$ のトレース $\mathrm{tr}(\textbf{A})$ は， $\textbf{A}$ の対角成分の和として定義されます．
行列の積のトレースには少し注意が必要なので，再掲します．2つの行列 $\textbf{A} \in \mathbb{R}^{m\times n}$ ， $\textbf{B} \in \mathbb{R}^{n\times m}$ を考えます．トレースの転置不変性を考慮すると，2つの行列の積に対しては，次のような順序の交換が可能です．

\mathrm{tr}(\textbf{AB}) = \mathrm{tr}(\textbf{BA})

両辺で行列のサイズが異なっていることに注意してください．
次に，3つの行列 $\textbf{A} \in \mathbb{R}^{m\times n}$ ， $\textbf{B} \in \mathbb{R}^{n\times p}$ ， $\textbf{C} \in \mathbb{R}^{p\times m}$ を考えます．3つの行列の積 $\textbf{ABC}$ に対しては， $\textbf{AB}$ と $\textbf{C}$ の積あるいは $\textbf{A}$ と $\textbf{BC}$ の積とみなすことで，次のような順序の交換が可能です．

\mathrm{tr}(\textbf{ABC}) = \mathrm{tr}(\textbf{CAB}) = \mathrm{tr}(\textbf{BCA})

ただし，次のような順序の交換はできません．

\mathrm{tr}(\textbf{ABC}) = \mathrm{tr}(\textbf{BAC})

右辺は行列のサイズが合わないのでそもそも積が定義できないのですが，仮に $\textbf{A}$ ， $\textbf{B}$ ， $\textbf{C}$ がすべて $n \times n$ 正方行列だったとしても，このような順序の交換はできません．

第6章幾何学的考察

ベクトルまたは行列の内積やノルム，正規直交基底といった重要な概念を導入し，代数と幾何の橋渡しをします．
内積はノルムを誘導します． $m\times n$ 行列の線形空間 $\mathcal{V}$ の中の行列 $\textbf{A}$ のノルムは

||\textbf{A}|| = (\textbf{A} \cdot \textbf{A})^{1/2}

で定められますが，これは通常の内積の場合，

||\textbf{A}|| = \bigl(\mathrm{tr}(\textbf{A}' \textbf{A})\bigr)^{1/2} = \Biggl(\sum_{i=1}^m \sum_{j=1}^na_{ij}^2 \Biggr)^{1/2}

とFrobeniusノルムを誘導します．これらの概念は計量空間やノルム空間といった話題に関係してきますが，この本ではそこには立ち入りません．
また，Schwarzの不等式（三角不等式の基礎となります）やGram-Schmidtの直交化も扱います．さらに，Gram-Schmidtの直交化から，任意の行列 $\textbf{A}$ を直交行列 $\textbf{Q}$ と上三角行列 $\textbf{R}$ の積に分解するQR分解というアルゴリズムが導かれます．QR分解は，最小二乗法や固有値計算に用いられる重要なアルゴリズムです．

第7章線形系 ―― 無矛盾性と両立性

次章で逆行列を導入する準備として，線形系 $\textbf{AX}=\textbf{B}$ に解が存在するための条件を考えます．

第8章逆行列

前章で考えた線形系 $\textbf{AX}=\textbf{B}$ で，行列 $\textbf{A}$ が非特異なら，逆行列 $\textbf{A}^{-1}$ が存在して， $\textbf{X}=\textbf{A}^{-1}\textbf{B}$ と実際に解を求めることができます．ここではその計算方法などについては論じず，分割行列の逆行列について多くのページを割いています．その中で出てくるSchurの補元は，後でも度々登場するので要確認です．

第9章一般逆行列

逆行列を，線形系で係数行列が特異な（すなわち逆行列を持たない）場合に拡張します． $m\times n$ 行列 $\textbf{A}$ の一般逆行列とは，

\textbf{AGA} = \textbf{A}

を満たす $n\times m$ 行列 $\textbf{G}$ のことを言います．非特異行列の逆行列がただ1つに定まるのに対し，特異行列の一般逆行列は無数に存在しますが，特異行列 $\textbf{A}$ の任意の一般逆行列 $\textbf{G}$ に対して $\textbf{X} = \textbf{GB}$ は線形系 $\textbf{AX}=\textbf{B}$ の解になります．また，どんな行列にも少なくとも1つの一般逆行列が存在します．以下では，行列 $\textbf{A}$ の一般逆行列を $\textbf{A}^-$ と書きます．本の中では実際に小さな行列を使って具体例が示されています．

第10章冪等行列

正方行列 $\textbf{A}$ が

\textbf{A}^2 = \textbf{A}

を満たすとき， $\textbf{A}$ を冪等行列と呼びます．第12章で確認する通り，冪等行列は射影という幾何学的な操作と密接な関係を持っています．
本章はいくつかの興味深い性質を導出して終わります．例えば，冪等行列 $\textbf{A}$ は

\textbf{AAA} = \textbf{A}

を満たすので，自身が一般逆行列となります．また，階数とトレースが一致します．

\mathrm{rank} (\textbf{A} )= \mathrm{tr}(\textbf{A})

第11章線形系 ―― 解

第7章の続きです．逆行列などの必要な道具が揃ったので，今度は線形系の解の公式や解空間について論じます．
線形系 $\textbf{AX}=\textbf{B}$ の解の集まりを解集合と呼びます．同次線形系 $\textbf{AX}=\textbf{0}$ の解集合は線形空間をなすので，解空間と呼びます．また，列ベクトル $\textbf{x}$ に関する同次線形系 $\textbf{Ax}=\textbf{0}$ の解空間を行列 $\textbf{A}$ の零空間 (null space) と呼び， $\mathcal{N}(\textbf{A})$ と表します．これを式で書くと， $\textbf{A} \in \mathbb{R}^{m \times n}$ に対して，

\mathcal{N}(\textbf{A}) = \{\textbf{x}\in \mathbb{R}^{n \times 1} ~|~ \textbf{Ax}=\textbf{0} \}

となります．
次に，線形系の解の一般系を考えます．同次線形系 $\textbf{AX}=\textbf{0}$ の一般解は， $\textbf{Y}$ を適当な行列として，

\textbf{X}^* = (\textbf{I}-\textbf{A}^-\textbf{A})\textbf{Y}

で与えられます．非同次線形系の一般解は，対応する同時線形系の一般解 $\textbf{Z}^*$ と非同次線形系の特殊解 $\textbf{X}_0$ の和として与えられます．
また，同次線形系 $\textbf{Ax}=\textbf{0}$ の解の個数 $\mathrm{dim}(\mathcal{N}(\textbf{A}))$ について，階数・退化次数の定理 (rank-nullity theorem) とも呼ばれる次の式が成り立ちます．

\mathrm{dim}(\mathcal{N}(\textbf{A})) = n - \mathrm{rank} (\textbf{A} )

なお，この本では線形変換について最後の第22章で簡単に取り上げるのみですが，線形変換 $T:\mathcal{V} \rightarrow\mathcal{W}$ に対しても同様の等式が成り立ちます．

\mathrm{dim}( \mathrm{Ker}(\textbf{A}) ) = \mathrm{dim}(\mathcal{V}) - \mathrm{dim}( \mathrm{Im}(\textbf{A}) )

第12章射影と射影行列

第10章に関連して，射影を導入しその統計に関する側面について論じます．
$\mathcal{U}$ を線形空間 $\mathcal{V}$ の部分空間とします．任意の行列 $\textbf{Y}\in \mathcal{V}$ に対して， $(\textbf{Y}-\textbf{Z}) \perp \mathcal{U}$ を満たす一意の射影 $\textbf{Z}\in \mathcal{U}$ が存在します．また，行列 $\textbf{X}$ の列が $\mathcal{U}$ を張る場合，

\textbf{P}_\textbf{X} = \textbf{X}(\textbf{X}'\textbf{X})^-\textbf{X}'

を $\mathcal{U}$ に対する射影行列と呼び， $\textbf{P}_\textbf{X}\textbf{Y}$ は $\textbf{Y}$ の $\mathcal{U}$ への射影となります．
射影は幾何的な意味を考えると理解しやすいです．本の中では2次元と3次元の場合の具体例が図とともに示されています．射影行列が冪等であることは簡単に示せますが，これも幾何的な意味を考えれば直感的に理解できると思います．
射影は最小二乗問題とも関係があります． $\mathcal{U}$ を線形空間 $\mathcal{V}$ の部分空間とし， $\textbf{Y}\in \mathcal{V}$ とします． $\textbf{W}\in \mathcal{U}$ に対して， $||\textbf{Y}-\textbf{W}||^2$ は $\textbf{W}$ が $\textbf{Y}$ の $\mathcal{U}$ への射影であるときに最小値をとります．このとき， $\textbf{W}\perp(\textbf{Y}-\textbf{W})$ より，その最小値は，

||\textbf{Y}-\textbf{W}||^2 = \textbf{Y}\cdot (\textbf{Y}-\textbf{W})

です．

第13章行列式

ここでようやく，正方行列に対して定義されるスカラー値である行列式 (determinant) が登場します．行列式の重要性や統計との関わりは言うまでもないでしょう．本章ではその定義，性質，余因子を使った計算方法などについて述べています．
行列式は高校時代からの長い付き合いですが，厳密には要素どうしの正対/負対（あるいは転倒数）と順列を使って，ややこしい定義がなされます．定義とともに詳細は書きませんが，「列（行）同士を交換すると行列式の符号が反転する」といった基本変形の導出も行います．
また， $|\textbf{AB}|=|\textbf{A}||\textbf{B}|$ から，次の事実を得ます．

直交行列の行列式の絶対値は1に等しい
逆行列の行列式は，元の行列の行列式の逆数に等しい

最後に，余因子という概念を導入します． $n \times n$ 行列 $\textbf{A}=\{ a_{ij} \}$ から要素 $a_{ij}$ を含む行と列，すなわち第 $i$ 行と第 $j$ 列を削除して得られる部分行列を $\textbf{A}_{ij}$ とします．このとき， $a_{ij}$ の余因子 (cofactor) を

\alpha_{ij} = (-1)^{i+j}|\textbf{A}_{ij}|

と定義します．すると， $\textbf{A}$ の行列式は， $\textbf{A}$ のある行または列の $n$ 個の要素について余因子展開が可能です．すなわち，任意の行に対して（ $i=1,\ldots,n$ ），

|\textbf{A}| = \sum_{j=1}^n a_{ij}\alpha_{ij}

です（列に対しても同様）．さらに， $n \times n$ 行列 $\textbf{A}=\{ a_{ij} \}$ に対して，対応する余因子からなる行列（余因子行列）の転置を随伴行列 (adjoint matrix) と呼びます．式で書くと，

\mathrm{adj} (\textbf{A} ) = \{ \alpha_{ji} \}

です．この定義より

\textbf{A} ~\mathrm{adj} (\textbf{A} ) = \mathrm{adj} (\textbf{A} )\textbf{A} = |\textbf{A}|\textbf{I}_n

が導け， $\textbf{A}$ が非特異なときに，行列式と随伴行列から逆行列を計算することができます．

第14章線形形式，双線形形式，二次形式

行列の二次形式や正定値性，そして行列の分解について議論します．12の節からなる長い章なので，内容をかなり絞って書きます．
$n \times n$ 行列 $\textbf{A}$ が任意の $\textbf{x}\in \mathbb{R}^n$ に対して $\textbf{x}'\textbf{Ax} \geq0$ を満たすとき， $\textbf{A}$ が非負定値 (nonnegative definite) であると言います．特に， $\textbf{x}'\textbf{Ax} >0$ を満たすとき， $\textbf{A}$ が正定値 (positive definite) であると言います．非負定値であるが正定値でないとき， $\textbf{A}$ が半正定値 (positive semidefinite) であると言います．
基本的な性質を次にまとめます．

正定値行列の対角成分はすべて正であり，半正定値行列の対角成分はすべて非負です
（ここで固有値との関係を説明するのが自然だと思いますが，固有値はなぜか第21章まで出てきません．）
任意の正定値行列は非特異です．ただし，逆は成り立ちません．

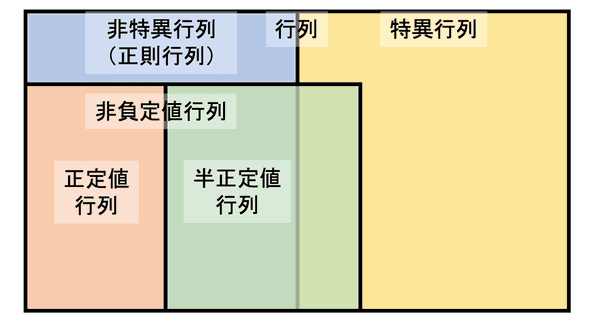
さて，ここまでに登場した様々な行列の関係がわかりづらくなってきたので，ベン図にまとめてみました．半正定値行列が非特異行列と特異行列にまたがっているのがポイントです．なお，この本では行列は実数値のみからなるとします．

* 正定値性に関する用語は文献によって定義が異なるようなので注意が必要です．非負定値・正定値・半正定値を対称行列に限って定義する文献もあるそうです．また，この本で言うところの非負定値のことを「半正定値」と定義する文献もあるそうです．

次に，ある条件を満たす正方行列 $\textbf{A}$ を，単位下三角行列 $\textbf{L}$ ，対角行列 $\textbf{D}$ ，単位上三角行列 $\textbf{U}$ の積に分解するLDU分解から，任意の対称正定値行列 $\textbf{A}$ を対角成分が正の上三角行列 $\textbf{T}$ を用いて

\textbf{A} = \textbf{T}'\textbf{T}

と一意に分解するCholesky分解を導きます．LDU分解やCholesky分解は，逆行列の計算などに利用できます．
対称行列 $\textbf{A}$ の正定値性および非負定値性に関しては，次の同値が成り立ちます．

$\textbf{A}$ のすべての主部分行列の行列式が非負 $\iff$ $\textbf{A}$ は非負定値
$\textbf{A}$ のすべての首座部分行列の行列式が正 $\iff$ $\textbf{A}$ は正定値

また，対称正定値行列 $\textbf{A}$ に関する双線形形式 $\textbf{x}'\textbf{Ay}$ は内積の公理を満たします．これは，内積の演算の内部に， $\textbf{A}$ のCholesky分解で得られる行列 $\textbf{T}$ による線形変換を含めることに他なりません．このように内積を定義したとき，射影行列も伴って次のように変わります．

\textbf{P}_{\textbf{X},\textbf{A}} = \textbf{X}(\textbf{X}'\textbf{AX})^-\textbf{X}'\textbf{A}

第15章行列の微分

上巻の最後は，統計学でしばしば登場する行列の微分を扱います．具体的には，微分の定式化から，各種スカラー/ベクトル/行列の微分，鎖律，いくつかの積分を含みます．
重要な結果はたくさんあるのですが，そのうち最も基本的なものだけを記号の定義なしで書くと，

\frac{\partial (\textbf{x}'\textbf{A})}{\partial \textbf{x}} = \frac{\partial (\textbf{A}'\textbf{x})}{\partial \textbf{x}} = \textbf{A}

\frac{\partial (\textbf{x}'\textbf{Ax})}{\partial \textbf{x}} = (\textbf{A}+\textbf{A}')\textbf{x}

\frac{\partial (\textbf{AB})}{\partial \textbf{x}} = \frac{\partial \textbf{A}}{\partial \textbf{x}} \textbf{B} + \textbf{A}\frac{\partial \textbf{B}}{\partial \textbf{x}}

\frac{\partial (\textbf{A}^{-1})}{\partial \textbf{x}} = - \textbf{A}^{-1}\frac{\partial \textbf{A}}{\partial \textbf{x}} \textbf{A}^{-1}

などがあります． $\mathrm{tr}(\textbf{AX})$ や $\mathrm{det}(\textbf{X})$ などの行列 $\textbf{X}$ の関数をその行列自身 $\textbf{X}$ で微分する際は， $\textbf{X}$ に制約があるか否か（例えば対称行列など）によって結果が変わるので注意が必要です．

第16章クロネッカー積とvec作用素とvech作用素

直積やテンソル積とも呼ばれるKronecker積，行列をベクトルに再配列するvec作用素，行列の対角成分とその上に位置する要素をベクトルに再配列するvech作用素を導入します．これらを使うと，第15章で扱ったような行列の微分などの計算で見通しがよくなるそうです．

第17章部分空間の共通部分と和

線形空間 $\mathbb{R}^{m\times n}$ の部分空間 $\mathcal{U}, \mathcal{V}$ に対して，部分空間の和を

\mathcal{U}+ \mathcal{V} = \{ \textbf{A}+\textbf{B} ~|~ \forall \textbf{A} \in\mathcal{U}, \forall \textbf{B} \in\mathcal{V} \}

と定義します．また， $\mathcal{U} \cap \mathcal{V}=0$ のとき， $\mathcal{U}$ と $\mathcal{V}$ は本質的に互いに素 (essentially disjoint) であると言います．さらに，このときの和を直和 (direct sum) と呼び， $\mathcal{U} \oplus \mathcal{V}$ と書きます．これらの演算と次元の間には，

\mathrm{dim}(\mathcal{U} + \mathcal{V}) = \mathrm{dim}(\mathcal{U}) + \mathrm{dim}(\mathcal{V}) - \mathrm{dim}(\mathcal{U} \cap \mathcal{V})

が成り立ちます．

第18章行列の和（と差）

$\textbf{R}+\textbf{STU}$ の形で表される行列の行列式，逆行列，階数を始めとして，計算上便利な公式を多数示します．

第19章線形制約の下での（ $n$ 個の変数に関する）二次多項式の最小化

線形制約のある $n$ 変数二次関数の最小化について，Lagrangeの未定乗数法と第15章の結果を用いて考えます．

第20章ムーア―ペンローズ形逆行列

無数に存在する一般逆行列の中でも，Moore-Penrose形逆行列という特別な一般逆行列について考えます．
任意の $m\times n$ 行列 $\textbf{A}$ は，次の条件を満たす一意な $n\times m$ のMoore-Penrose形逆行列 $\textbf{A}^+$ を持ちます．

$\textbf{AA}^+\textbf{A}=\textbf{A}$
$\textbf{A}^+\textbf{AA}^+=\textbf{A}^+$
$(\textbf{AA}^+)' = \textbf{AA}^+$
$(\textbf{A}^+\textbf{A})' = \textbf{A}^+\textbf{A}$

$\textbf{A}$ が非特異なときは $\textbf{A}^+=\textbf{A}^{-1}$ であり， $\textbf{A}$ が最大列階数のときは

\textbf{A}^+=(\textbf{A}'\textbf{A})^{-1}\textbf{A}'

となります．
線形系 $\textbf{Ax}=\textbf{b}$ に対して， $\textbf{A}^+\textbf{b}$ は最小ノルム解を与えます．

第21章固有値と固有ベクトル

満を持して，固有値と固有ベクトル，そして特異値分解など統計や機械学習で頻出の概念を導入します．この章も長いので，内容をかなり絞って書きます.
まず，正方行列 $\textbf{A}$ のある固有値 $\lambda$ に対して， $\mathrm{dim}[\mathcal{N}(\textbf{A}-\lambda\textbf{I})]$ を $\lambda$ の幾何学的重複度と呼びます． $\lambda$ の特性方程式の解としての重複度を $\lambda$ の代数的重複度と呼びます．これら2種類の重複度は一般に一致せず，任意の固有値に対して（幾何的重複度） $\leq$ （代数的重複度）という関係が成り立ちます．行列 $\textbf{A}$ は幾何学的重複度を含めた固有値の数だけ互いに線形独立な固有ベクトルを持ちます．
そして， $n\times n$ 非特異行列 $\textbf{Q}$ の各列が $\textbf{A}$ の固有ベクトルであるときかつそのときに限って， $\textbf{A}$ はその固有値を並べた対角行列に $\textbf{Q}$ で対角化されます．

\textbf{Q}^{-1}\textbf{AQ} = \mathrm{diag}(\lambda_1, \ldots\lambda_n)

特に，任意の対称行列は $\textbf{Q}$ で直交対角化されます．

\textbf{Q}'\textbf{AQ} = \mathrm{diag}(\lambda_1, \ldots\lambda_n)

このとき， $\textbf{A}$ のノルムは簡単に計算できます．

||\textbf{A}|| = (\mathrm{tr}(\textbf{A}'\textbf{A}))^{1/2} = \Biggl(\sum_{i=1}^n\lambda_i^2\Biggr)^{1/2}

特別な行列の固有値の性質を次に挙げます．

直交行列の固有値は $1$ または $-1$ です
非負定値行列の固有値はすべて非負です
正定値行列の固有値はすべて正です

最後に，特異値分解を導出します．階数 $r$ の任意の $m\times n$ 行列 $\textbf{A}$ に対して， $m\times m$ 直交行列 $\textbf{P}$ ， $n\times n$ 行列 $\textbf{Q}$ ，正の対角要素を持つ $r\times r$ 対角行列 $\textbf{D}_1$ が存在し， $\textbf{A}$ を次のように分解できます．

\textbf{A} = \textbf{P}\left( \begin{array}{rr} \textbf{D}_1 & \textbf{0}\\ \textbf{0} & \textbf{0} \\ \end{array} \right) \textbf{Q}' = \textbf{P}_1\textbf{D}_1\textbf{Q}_1'

ただし， $\textbf{P}_1$ ， $\textbf{Q}_1$ はそれぞれ $\textbf{P}$ ， $\textbf{Q}$ の先頭 $r$ 列からなる行列とします． $\textbf{D}_1$ の正の対角要素は， $\textbf{A}'\textbf{A}$ （ $\textbf{AA}'$ ）の $r$ 個の正の固有値の正の平方根に一致します．これらのことを特異値 (singular value) と呼びます． $\textbf{Q}_1$ （ $\textbf{P}_1$ ）の列は $\textbf{A}'\textbf{A}$ （ $\textbf{AA}'$ ）の $r$ 個の正の固有値に対応する固有ベクトルです．また，小さい特異値を $0$ とすることで $r$ よりも小さな行列の積で $\textbf{A}$ を近似することができます．

第22章線形変換

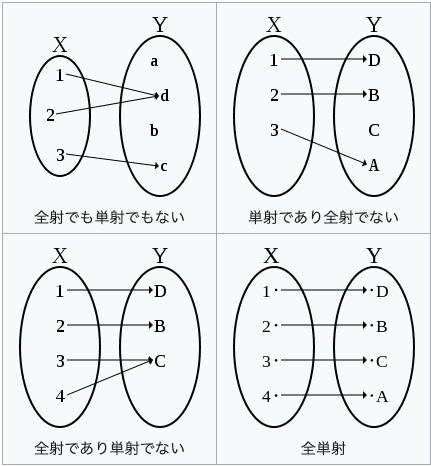
これまで行列とベクトルまたは行列同士の積として考えてきた計算を，線形変換というより抽象化された概念で捉え直します．教科書によっては序盤ないし中盤から線形変換を扱うものもありますが，この本では最後に視座を上げるような構成をとっています．
用語としては，中への変換（全射），上への変換（単射），1-1変換（全単射） が新たに登場します．これらについては，Wikipediaのこの図がわかりやすいと思います．

誤植が疑われる箇所

最後に，誤植が疑われる箇所を記しておきます．私は2019年発行の第7刷で読みました．原著との比較はしていません．

上巻

p55: 補助定理4.5.10の1つ目の同値の右辺が「 $\mathcal{C}(\textbf{B}) \subset \mathcal{C}(\textbf{E})$ 」となっていますが，正しくは「 $\mathcal{C}(\textbf{A}) \subset \mathcal{C}(\textbf{E})$ 」だと思われます
p164: 定理11.2.1の証明の後半「よって， $\textbf{Y}=\textbf{X}^*$ に対して」とありますが，「 $\textbf{Y}=\textbf{X}^*$ 」ではなく単に「 $\textbf{Y}$ 」だと思われます
p229: 式(5.3)の最左辺は $\sum_{j=1}^n a_{ij}\alpha_{i'j}$ ，すなわち総和の添字が $i$ ではなく $j$ だと思われます
p230: 式(5.4)の左から2番目の辺の第1項は，正しくは $a_{1j}\alpha_{1j'}$ だと思われます
p274: 定理14.5.9の証明で，「系14.4.7」と参照されているところは「系14.5.7」の誤りだと思われます
p284: 式(5.20)の説明で「（対角）行列 $\textbf{D}$ の非対角要素」とありますが，正しくは「（対角）行列 $\textbf{D}$ の非ゼロ対角要素」だと思われます
p307: 準ノルムの説明で，「量 $(\textbf{A}\cdot \textbf{B})^{1/2}$ 」とありますが，正しくは「量 $(\textbf{A}\cdot \textbf{A})^{1/2}$ 」だと思われます
p313: 「projection of $\textbf{y}$ on $\mathcal{U}$ with respect to $\textbf{W}$ 」とありますが， $\mathcal{U}$ の後ろのスペースが抜けています
p366: 式(8.3)の右辺は，正しくは $[\mathrm{adj}(\textbf{X})]'$ だと思われます

下巻

p75: 式(4.11)の右辺第3項は，正しくは $\mathrm{dim}[\mathcal{R}(\textbf{A}) \cap \mathcal{R}(\textbf{B})]$ だと思われます
p223: 「 $\textbf{A}$ の幾何学的重複度は $1$ に過ぎない」とありますが，厳密には「 $\textbf{A}$ の固有値 $1$ の幾何学的重複度は $1$ に過ぎない」と書くべきです
p228: 補助定理21.2.1の証明中の式の左から3番目の辺の「 $\textbf{I}$ 」は，次元を明示して「 $\textbf{I}_{n_{i}}$ 」と書いたほうが親切です．
p244: 定理21.5.10の証明中の式は，最左辺を除くすべてで全体を $1/2$ 乗する必要があります
p267: 「同様に， $\textbf{Q}$ の $n$ 個の列は（中略）残りの $m-r$ 個の列から成る」とありますが，「 $m-r$ 個」ではなく「 $n-r$ 個」だと思われます
p291: 定理21.A.3で「実数 $x$ は $p(x)$ の根である」とありますが，正しくは「実数 $c$ は $p(x)$ の根である」だと思われます

Written by Shion Honda. If you like this, please share!

Hippocampus's Garden

書評『統計のための行列代数』

はじめに