Different Measures of Feature Importance Behave Differently
September 05, 2020 | 7 min read | 3,443 views
Feature importance is a helpful indicator when deciding which features are necessary and which are not. But it can be misleading in tricky situations, such as when some features are strongly correlated with each other, as discussed in [1-3]. In this post, I inspect the behaviors of various importance measures in tricky situations and compare them, including some topics such as LightGBM’s built-in importance and scikit-learn’s permutation importance function.
Popular Importance Measures
First of all, I summarize some popular importance measures to compare in this post: Gini importance, split importance, drop-column importance, and permutation importance.
| Feature importance | Applicable Models | Needs validation set | Needs re-training |
|---|---|---|---|
| Gini | Tree-based model | No | No |
| Split | Tree-based model | No | No |
| Drop-column | Any model | Yes | Yes |
| Permutation | Any model | Yes | No |
This section briefly review the definition of these metrics. If you are already familiar with them, please skip to the experiment section.
Gini Importance
In tree-based models, each node split the data from its parent node on the feature that gives the greatest improvement in Gini impurity. Let’s say the node has the child nodes and . Now, the node ’s improvement in Gini impurity is:
where denotes Gini impurity at the node and the ratio of the node ’s sample size to the total sample size. Gini importance of feature is defined as the sum of the impurity improvement of the nodes using the feature.
Gini importance is used in scikit-learn’s tree-based models such as RandomForestRegressor and GradientBoostingClassifier. You can call it by model.feature_importances_ or something like that.
Split Importance
Split importance is also a measure of feature importance for tree-based models. It simply counts how many times the nodes split on the feature. It assumes that the more important the feature is, the more times it is split. This sounds naive after introducing Gini importance, but it is actually used in LightGBM by default! You have perhaps used it before without knowing it.
Above two measures are computed when the training is over, so you don’t need any out-of-bag validation set or re-training.
Drop-column Importance
Drop-column importance is a model-agnostic measure stemming from a simple idea: if a feature is not important, training without it won’t degrade the model’s performance. Drop-column importance is computed by the following steps:
- Train a model with all features
- Measure baseline performance with a validation set
- Select one feature whose importance is to be measured
- Train a model from scratch with all features but the selected one
- Measure performance with a validation set with the selected feature dropped
- The importance of the selected feature is the performance degradation from the baseline
- Iterate 3 through 6 for all features
Though the idea behind this algorithm is easy to understand, its computational cost is higher than other importance measures because it requires re-training as many times as the number of features.
Permutation Importance
Permutation importance is also model-agnostic and based on the similar idea to the drop-column but doesn’t require expensive computation. It is computed by the following steps:
- Train a model with all features
- Measure baseline performance with a validation set
- Select one feature whose importance is to be measured
- Measure performance with a validation set with the selected feature shuffled
- The importance of the selected feature is the performance degradation from the baseline
- Iterate 3 through 5 for all features
It is supported by scikit-learn v0.22 or later and can be easily called by permutation_importance(model, X_val, y_val) or something like that.
Random Target
The experiment part consists of two sections. In the first section, the target variable is independent fr the explanatory variables; In the other, it isn’t. So, in this section, I consider five explanatory variables that are i.i.d. samples from the standard normal distribution and one target variable that is also i.i.d.
Obviously, the target variable is never explained by the explanatory variables.
I compared the four importance measures in the following four cases:
- Control. I have’t change anything from the above settings.
- Different cardinalities. I rounded to the third decimal place, to the second, and so on.
- Duplicated columns. I copied to .
- Columns with colinearity. I re-assigned to , where . is no more independent from but still identically distributed.
For each importance measure, I trained a LightGBM regressor with the default hyperparameters for 100 times and plotted its histogram. The training set contains 1,000 samples and the validation set, if necessary, contains 200 samples.
The source code used for the experiments is available at https://github.com/shionhonda/feature-importance/.
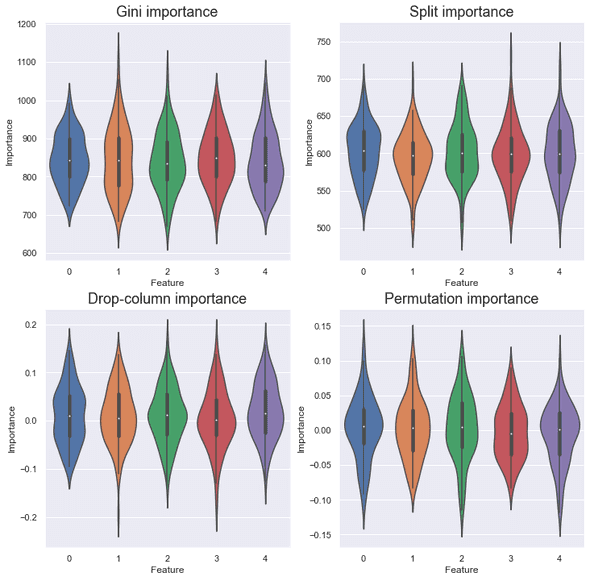
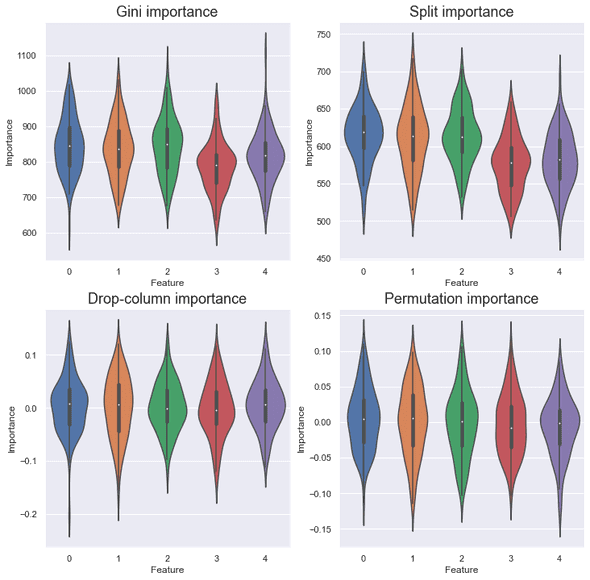
Control
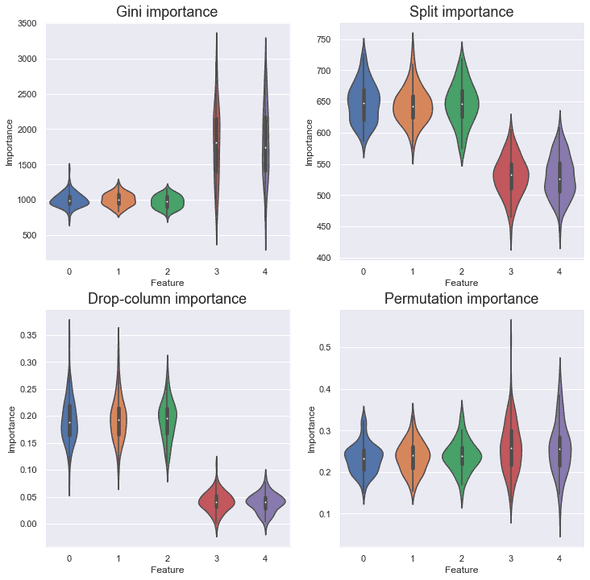
As expected, for all the importance measures, each feature contributed equally.
But ideally, the features should have no contribution. Why the scores are not zero for Gini and split importance? This is because they don’t use a validation set and simply reflect the result of training. You don’t trust training accuracy, right?
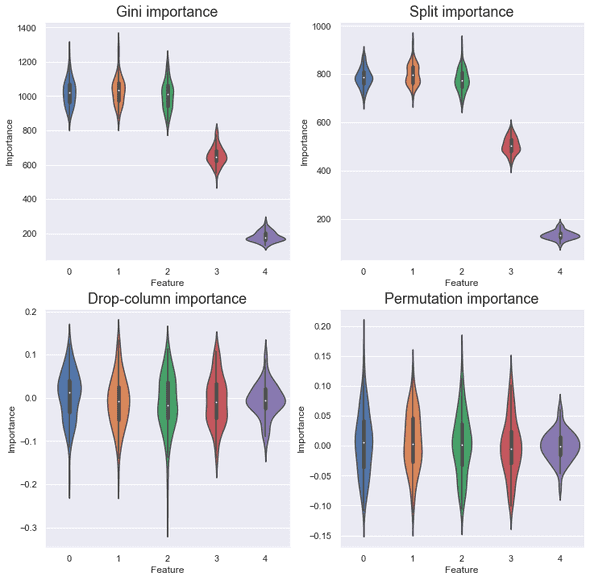
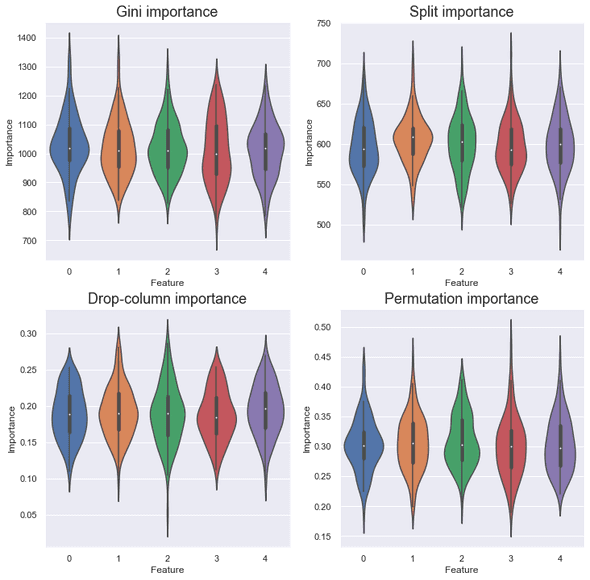
Cardinality
This setting changed the result dramatically. , which has the lowest cardinality with the values , made little contributions in terms of Gini and split importance. It looks rounding to the third or second decimal place didn’t change the cardinality very much. Also, it is worth noting that the variance of the score of is smaller than other variables in drop-column and permutation importance.
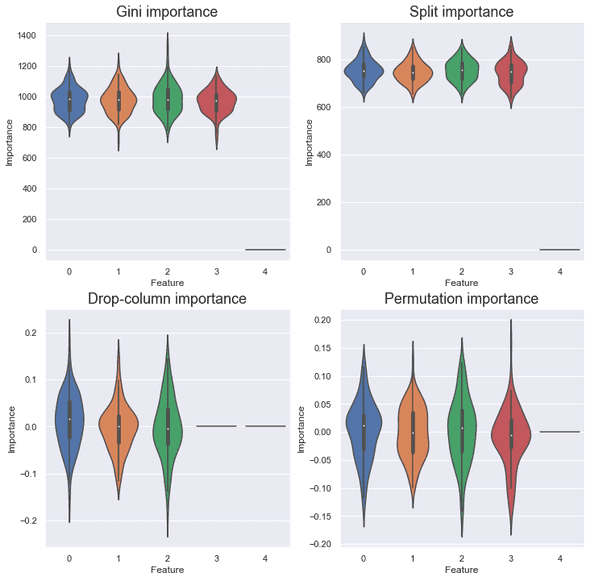
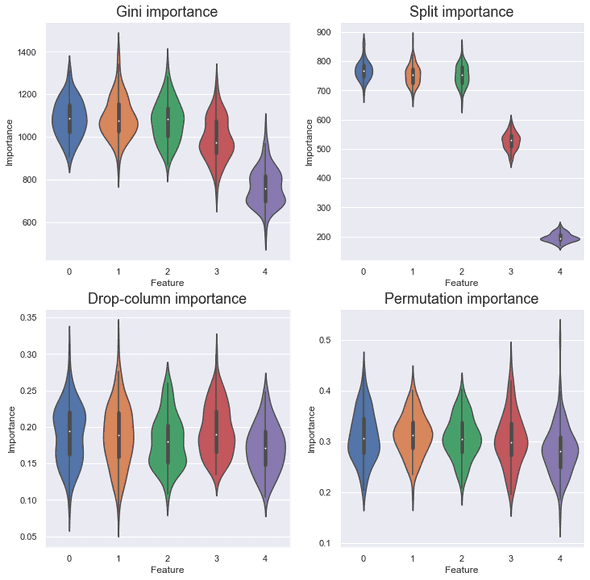
Duplication
The duplicated did not contribute at all for all the importance measures. This is natural because the model can get all the information of from and vice versa. I suppose the broken symmetry came from the order of features (the column order matters sometimes!). Drop-column importance treats features equally so the contribution of is also zero.
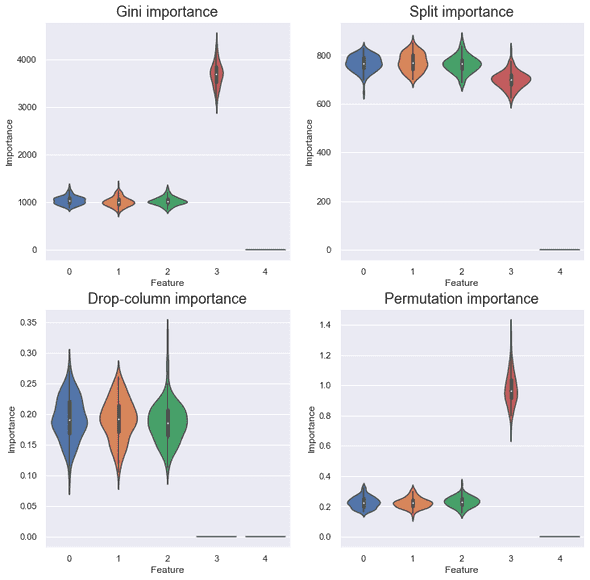
Colinearity
In the colinearity setting of Gini and split importance, it is observed that and fought for contributions and resulted in the less importance than the other features. This tendency is hardly seen in the drop-column and permutation importance.
Synthetic Target
In the last part, I inspected the behavior of the four importance measures when predicting the random target, but this may be too far from reality. So, this part assumes the target value as the simple average of the explanatory variables with a noise term.
Note that the distribution of is the same as the one in the last part.
Control
The result is again as expected. This time, the scores of drop-column and permutation importance are all positive.
Cardinality
The overall trend is the same as the last part. Now it can be said that drop-columns and permutation importance are robust to differences in cardinality.
Duplication
Surprisingly, according to the Gini and permutation importance, the duplicated is more important than , , and . Moreover, you’ll find the opposite relationship in the split importance.
The former phenomenon is explained by considering that the LightGBM model ignores and is produced by the following equation:
Now it’s clear that is “important”, but I don’t figure out why it is “less important” in split importance. I appreciate any comments about this result😄
Colinearity
The overall trend is the same as the duplication setting, but the variance of the scores of and are very large for Gini importance.
Concluding Remarks
In this post, I compared the behaviors of different feature importance measures in some tricky settings.
Take-home messages:
- Drop-column and permutation importance are robust to differences in cardinality
- Gini and split importance can lead to different results when colinearity is involved
- I recommend using permutation importance as a starter because it’s robust and fast
There are other importance measures such as SHAP and null importance, but I leave them for future work.
References
[1] 特徴量重要度にバイアスが生じる状況ご存知ですか? - 学習する天然ニューラルネット
[2] Terence Parr, Kerem Turgutlu, Christopher Csiszar, and Jeremy Howard. ”Beware Default Random Forest Importances“. Explained.ai. 2018.
[3] Permutation Importanceを使って検証データにおける特徴量の有用性を測る - Qiita
![[object Object]](/static/2d0f4e01d6e61412b3e92139e5695299/e9fba/profile-pic.png)
Written by Shion Honda. If you like this, please share!